Ingeniero Mecánico

Obtuve mi título profesional de ingeniero mecánico mediante el trabajo de tesis titulado: “Desarrollo e implementación de una aplicación computacional para el cálculo de componentes de sistemas de transmisión de potencia utilizando métodos de elementos finitos y analíticos”, el cual fue aprobado por unanimidad.

A continuación se detallan las principales diferencias respecto a tesis similares:

Digitalización de diagramas

Dado que para el cálculo y diseño de los componentes de un sistema de transmisión de potencia mecánico, resulta indispensable hacer uso de diagramas para determinar ciertos factores de suma importancia, lo cual consume tiempo y precisión, se ha visto por conveniente procesar dichos diagramas, para la obtención rapida y precisa de los señalados factores. Las ecuaciones utilizadas para dicho procesamiento son:

\[ \large x_{n_{a,b}} = \frac{x_{n_{b,a}} - x_{1_{b,a}}}{x_{2_{b,a}} - x_{1_{b,a}}}(x_{2_{a,b}} - x_{1_{a,b}}) + x_{1_{a,b}} \]

\[ \large y_{n_{a,b}} = \frac{y_{n_{b,a}} - y_{1_{b,a}}}{y_{2_{b,a}} - y_{1_{b,a}}}(y_{2_{a,b}} - y_{1_{a,b}}) + y_{1_{a,b}} \]

Configuración geométrica de la transmisión

La desalineación horizontal o vertical entre el eje del motor y el eje de transmisión del sistema resulta relevante al momento de determinar la magnitud, orientación y sentido de las fuerzas que se transmiten al último de los mencionados ejes. Los ángulos de descomposición de las fuerzas de transmisión se calculan con las siguientes expresiones:

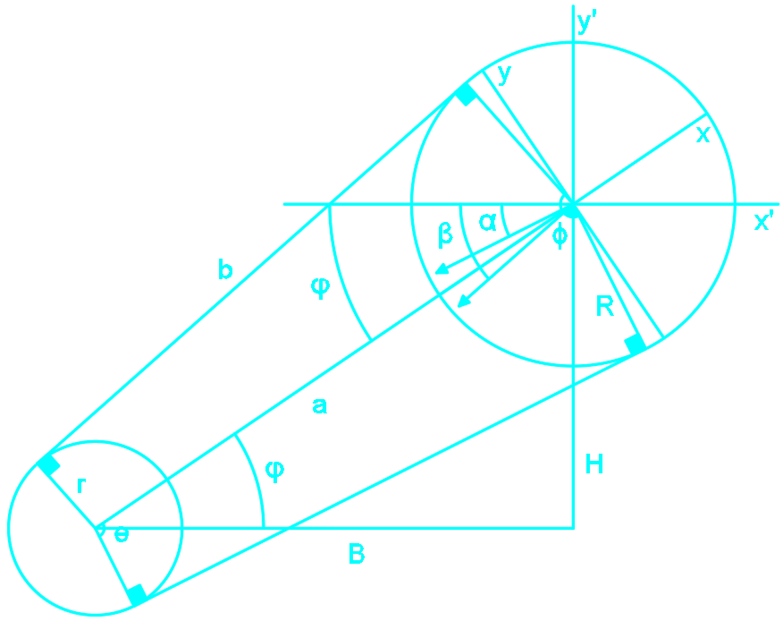
\[\large \phi = \arccos\left(\frac{R - r}{a}\right) \quad \varphi = \arccos\left(\frac{B}{a}\right)\]

\[\large \beta = 90 + \varphi - \phi \quad \quad \alpha = 2\varphi - \beta\]

Dependiendo del sentido de giro del motor, las fuerzas en los ejes X y Y se cálculan con las siguientes igualdades, dependiendo del sentido del motor:

\[ \large \text{Antihorario:} \quad \begin{array}{l} F_{x'} = F_{\max}\cos(\beta) + F_{\min}\cos(\alpha) \\ F_{y'} = F_{\max}\sin(\beta) + F_{\min}\sin(\alpha) \end{array} \]

\[ \large \text{Horario:} \quad \quad \quad \begin{array}{l} F_{x'} = F_{\min}\cos(\beta) + F_{\max}\cos(\alpha) \\ F_{y'} = F_{\min}\sin(\beta) + F_{\max}\sin(\alpha) \end{array} \]

Ejes de transmisión huecos

Para el análisis de ejes huecos, se ha considerado el efecto del orificio interior, en las propiedades geométricas del eje de transmisión. Dichas propiedades son:

Área \[A = \pi (R^2 - r^2)\]

Momento polar de inercia \[\large J = \frac{\pi (R^4 - r^4)}{2}\]

Primer momento de área \[\large I = \frac{\pi (R^4 - r^4)}{4}\]

Segundo momento de área \[\large Q = \frac{2(R^3 - r^3) \sin ^3\alpha}{3}\]

Espesor \[t = 2(R - r)\sin \alpha\]

Cálculo general de ejes de transmisión

Mediante el método de las integraciones concecutivas, se hace posible determinar las fuerzas cortantes, momentos flectores, deformaciones angulares y lineales presentes en el eje de transmisión. Las ecuaciones que describen dichos resultados, para cada tramo del eje, se han planteado de la siguiente manera:

Fuerzas cortantes:

\[ \large V_k(x) = - \sum_{i=1}^k F_i - w_i(x - x_i) - \sum_{i=1}^k w_{i-1}(x_i - x_{i-1}) \]

Momentos flectores:

\[ \large M_k(x) = -x\sum_{i=1}^k F_i - \frac{1}{2}w_i(x - x_i)^2 - x\sum_{i=1}^k w_{i-1}(x_i - x_{i-1}) + C_{1_i} + M_i \]

Deformaciones angulares:

\[ \large \theta_k(x) = \frac{- \frac{x^2}{2}\sum_{i=1}^k F_i - \frac{1}{6}w_i(x - x_i)^3 - \frac{x^2}{2}\sum_{i=1}^k w_{i-1}(x_i - x_{i-1}) + C_{1_i}x + M_ix + C_{2_i}}{E_iI_i} \]

Deformaciones lineales:

\[ \large y_k(x) = \frac{- \frac{x^3}{6}\sum_{i=1}^k F_i - \frac{1}{24}w_i(x - x_i)^4 - \frac{x^3}{6}\sum_{i=1}^k w_{i-1}(x_i - x_{i-1}) + \frac{C_{1_i}x^2}{2} + \frac{M_ix^2}{2} + C_{2_i}x + C_{3_i}}{E_iI_i} \]

Para k = 1 → T, donde T es el numero de tramos del eje de transmisión. Aplicando las condiciones de frontera correspondientes en dichas ecuaciones y considerando ademas a las ecuaciones referidas al equilibrio estático, siempre sera posible cálcular todas las incognitas presentes en el sistema de ecuaciones formulado. Esto significa que, sin importar el número de apoyos y cargas presentes en el eje de transmisión o sus propiedades, este se podra cálcular sin problemas.

Fuerzas cortantes en ejes de transmisión

En el analisis de rigidez y de vibraciones

Por medio de la teoría de Timoshenko, se incorporan los efectos de las fuerzas cortantes en el cálculo de las reacciones y deformaciones presentes en el eje de transmisión.

\[ \large k = \frac{EI}{L^3(1 + \varphi)} \left[ \begin{array}{cccc} 12 & 6L & -12 & 6L \\ 6L & (4 + \varphi)L^2 & -6L & (2 - \varphi)L^2 \\ -12 & -6L & 12 & -6L \\ 6L & (2 - \varphi)L^2 & -6L & (4 + \varphi)L^2 \end{array} \right] \]

Esto se debe a la presencia del siguiente factor (en contraste con la teoría de Euler y Bernoulli):

\[ \large \varphi = \frac{12EI}{K_sAGL^2} \]

Dentro del cual se encuentra el termino Ks, mas conocido como factor de área y depende del tipo de sección a analizar, y del material correspondiente a dicha sección.

\[ \large K_S = \frac{6(1 + \nu)(1 + m^2)^2}{(7 + 6\nu)(1 + m^2)^2 + (20 + 12\nu)m^2} \to m = \frac{r}{R} \quad \text{y} \quad \nu = 0.3 \]

En el analisis estático y dinámico

Los esfueros cortantes estáticos, independientemente de la teoria de cálculo utilizada, se computan por medio de la siguiente expresión:

\[ \large \tau_{\text{cortante}} = \frac{FQ}{It} \]

Los esfueros cortantes dinámicos, independientemente de la teoria de cálculo utilizada, se computan por medio de la siguiente expresión:

\[ \large \tau_{\text{medio cortante}} = \frac{2(R^2 + Rr + r^2)(F_y + F_z)}{3\pi(R^4 - r^4)} \]

\[ \large \tau_{\text{alternante cortante}} = \frac{2(R^2 + Rr + r^2)|F_y - F_z|}{3\pi(R^4 - r^4)} \]

Elementos de mayor estres en el eje de transmisión

A diferencia de los software modernos de diseño asistido por computadora, la aplicación desarrollada se basa en un análisis bidimiensional, por lo que era imperativo seleccionar un elemento a analizar para cada sección del eje. Ahora bien, dado que por su naturaleza y aplicación práctica, los esfuerzos flexionantes son mas relevantes que los esfuerzos cortantes, se opto por establecer que el elemento a analizar sera aquel en el cual se presente el esfuerzo flexionante máximo. En magnitud, el valor de dicho esfuerzo se calcula como:

\[ \large \sigma_{yz} = \frac{4R(M_y\sin \beta + M_z\cos \beta)}{\pi(R^4 - r^4)} \]

El máximo de la expresión anterior, se determina bajo el siguiente ángulo:

\[ \large \beta = \arctan\frac{M_y}{M_z} \]

En cuanto a la ubicación de dicho elemento, este se encontrara en el sector en el cual el sentido de los esfuerzos flexionantes y axiales coincidan, y desfasado en beta grados respecto de dicho sector. En este punto, cabe señalar que tanto los esfuerzos flexionantes y cortantes se suman, de manera independiente, cuando coinciden en su orientación.

Vibraciones en ejes de transmisión

Los limites en los cuales se encuentra comprendida la velocidad crítica del eje, se determinan mediante las ecuaciones de Rayleight y Ritz.

\[ \large \text{Límite inferior:}\quad \text{RPM} = \frac{30}{\pi}\sqrt{\frac{g}{\max(\delta_R)}} \]

\[ \large \text{Límite superior:}\quad \text{RPM} = \frac{30}{\pi}\sqrt{g\frac{\sum_{i=1}^T \rho_i A_i \int y_i dx}{\sum_{i=1}^T \rho_i A_i \int y_i^2 dx}} \]

Analisis de elementos bidimensionales de transmisión mediante elementos finitos

Se utilzan elementos triangulares de deformación constante (CST), donde cada uno de estos esta definido por tres pares de coordenadas, un área, un módulo de elasticidad, un coeficiente de Poisson y un espesor, a partir de los cuales se procede a formular la matriz de rigidez respectiva. Con las matrices de rigidez individuales se plantea la matriz de rigidez global, la cual, junto con las matrices de fuerzas y desplazamientos, se redimensionan en base a las condiciones de frontera, para posteriormente resolver el sistema general y determinar asi, las reacciones y desplazamientos en cada nodo de la malla, lo cual a su vez, permite calcular los esfuerzos a los cuales esta sometido el elemento que se requiera analizar.

\[\large [F]=[K][d] → [\sigma_x, \sigma_y, \tau_{xy}]\]